HPLC 컬럼은 튜빙 내에 입자크기가 5~10 ㎛인 충진물질(Stationary Phase)을 채워서 사용한다. 충진물질은 분리하고자 하는 물질에 따라 다양한 물질을 사용하며, 세부적인 내용은 2장을 참조하기 바란다. 튜빙은 600 psi보다 낮은 압력에서 유리관을 사용하기도 하지만 일반적으로 Stainlessless Steel로 만들어진다. 대부분의 HPLC 컬럼은 10~30 cm이며 내부 지금은 4~10 cm이다. 이 형태의 컬럼은 대개 40,000~60,000 이론단수/m를 가진다. 최근에는 내부지름이 1~4.6 mm 이고 이론단수가 100,000에 이르는 마이크로 컬럼을 사용하기도 한다.
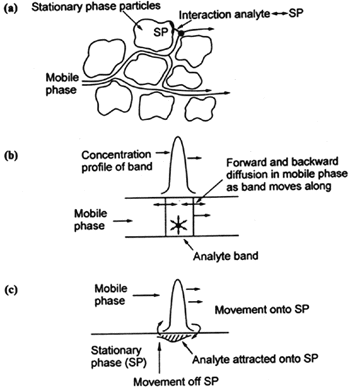
HPLC 컬럼에서 용리가 일어나는 동안 한 개의 용질 분자가 정지상과 이동상 사이에서 수많은 이동이 일어난다. 각 상에서 머무르는 시간은 아주 불규칙적이다. 한 상에서 다른 상으로의 이동은 에너지를 필요로 하는데 분자는 이 에너지를 주위에서 얻어야 한다. 따라서 어떤 분자는 주어진 상에서 머무르는 시간이 순간적이고, 어떤 분자는 머루르는 시간이 상대적으로 길 수도 있다. 컬럼 속에서 이동은 분자가 이동상 내에 있을 때에만 일어나며, 결과적으로 시료를 구성하고 있는 성분들의 이동속도는 그들이 정지상에 머무르는 시간에 따라 달라진다. 이들의 이동속도는 일반적으로 평균이동속도를 중심으로 대칭으로 퍼진 Gaussian Peak의 형태를 띠게 된다.
시료의 분리-용리띠의 퍼짐
1. 컬럼에서의 용리띠 퍼짐
컬럼에서 발생하는 퍼짐을 설명하는 주요한 두 가지 이론은 단이론(Plate theory)과 속도이론(Rate theory)이다.
(1) 단이론(Plate theory)
단이란 이론상의 단으로 컬럼의 내부가 수많은 크기가 동일한 분리층으로 구성되어 있다고 가정한다. 이러한 단에서는 최소한의 시료들의 분리가 일어나며, 단 수가 많다면 분리가 많이 일어나서 결과가 좋을 것이다. 이렇게 컬럼 내의 분리에 관여하는 단의 수를 이론단수(Number of theoretical plates, N)라 한다. N은 띠폭(band width)를 tW로 하고 피크가 기준선(혹은 바탕선:baseline)과 만나는 지점의 사이를 측정하여 얻는다. 이렇게 해서 가우스 분포곡선을 용리띠로 생각해서 수학적으로 근사한 관계를 얻을 수 있다.
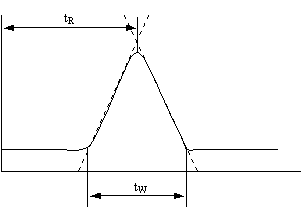
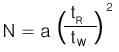 | a : constant depending on method used tR : retention time of peak tW : peak width |
동일한 조건(컬럼과 이동상, 유속, 온도, 시료 주입방법 등)에서는 크로마토그램의 어느 성분의 피크로부터 N값을 계산하든지 거의 일정한 값을 보이게 된다. 일반적으로 컬럼의 효율(Column efficiency)을 N값으로 표현하고 이러한 N값이 클수록 분리능은 높아지게 된다. 이러한 분리를 잘되게 하는 N을 증가시키는 방법에는 두가지가 있다.
① 컬럼의 길이 증가
컬럼의 단은 동일하고 일정한 간격을 가지고 있으므로 컬럼의 길이(L)를 증가하면 N은 증가한다. 하지만 길이를 증가시키면 tR과 tW도 따라서 증가하게 된다. 이 때 각각의 값들이 증가하는 정도를 보면 길이가 2배로 늘어났을 때 tR = L/U(1+ k')에서 알 수 있듯이 2배로 증가한다. 따라서 tW는 21/2배 증가하게 된다.
컬럼의 단은 동일하고 일정한 간격을 가지고 있으므로 컬럼의 길이(L)를 증가하면 N은 증가한다. 하지만 길이를 증가시키면 tR과 tW도 따라서 증가하게 된다. 이 때 각각의 값들이 증가하는 정도를 보면 길이가 2배로 늘어났을 때 tR = L/U(1+ k')에서 알 수 있듯이 2배로 증가한다. 따라서 tW는 21/2배 증가하게 된다.
② 정지상 입자의 크기를 감소 일반적으로 사용자가 입자의 크기를 감소할 수는 없고 더 작은 입자로 구성된 컬럼을 구입하여 사용하는 방법인데 이 경우 머무름 시간을 증가시키지 않고 N값을 증가시키는 방법이다. 컬럼길이를 증가하는 것보다는 효과적이다. 상품의 사양에 입자의 크기가 나오기는 하지만 이론적으로 입자의 크기는 컬럼의 길이를 N값으로 나눈 것이다. 이것을 이론단 해당높이(HETP : Height Equivalent to a Theoretical Plate)라고 부른다. 다시 말해서 HETP를 식으로 나타내면
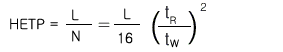
와 같다. 이 방법은 결국 HETP를 줄이는 결과를 가져오는데 이 방법은 길이(L)가 고정되고 tR은 증가되지 않으므로 결국에는 tW이 감소되어 좁은 피크를 얻게 되어 좋은 분리 결과를 가져오게 된다.
2) 속도이론(Rate theory)
HETP값이 이상적인 경우 0값을 보이지만 실제는 항상 시료들이 퍼짐현상을 보이게 되고 결국은 HETP 값은 항상 0보다 크게 되는 것에 관련하여 생각하는 것이다. 이러한 퍼짐현상은 앞에서 설명한 소용돌이 확산, 세로확산, 질량이동 현상의 3가지로 간단히 규정하고 HETP와의 관계를 식으로 보면 아래와 같다.
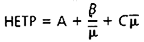
이 식은 네덜란드의 석유화학자 그룹이 수학적으로 유도한 것으로 van Deemter식이라 부른다. 이 식에서 HETP를 증가시키는 방법은 A항을 작게 B, C항은 적당한 유속으로 B와 C항의 합이 최소가 되도록 하여야 한다.
A : eddy diffusion
소용돌이 확산에 따른 사용한 컬럼의 계수로서 이동상의 속도와 관련없는 항목으로 아래 그림에서와 같이 분석시료가 다양한 경로로 진행함으로써 생긴다. 작고 균질한 입자를 사용하며, 균일한 충진을 하면 줄어들 수 있다.
B : longitudinal diffusion
세로확산에 따른 사용한 컬럼의 계수로서 이동상과 정 혹은 반대의 방향으로 생기는 확산을 말한다. 이동상의 유속과 반비례하므로이동상이 액체이면 확산은 약 10-5정도이므로 LC에서는 무시할 수 있으나 GC에 있어서는 carrier gas의 속도와 종류에 따라 영향을 미치게 된다.
C : mass transfer
질량이동에 따른 사용한 컬럼의 계수로서 평형의 불충분으로 인해서 생기는 항목으로정지상의 기하학적 구조, 분배계수 및 두 상에서의 확산속도 등의 영향을 받는다. 정지상의 두께(컬럼의 지름)를 얇게 하고 분리 온도를 높여 빠른 평형을 가능하게 하면 이를 줄일 수 있다. GC의 경우 film thickness가 작아지면 이 항목으로 인한 band broadening이 발생할 확률이 작아진다. 또한 유속을 낮추면 평형에 충분한 시간을 주게 되므로 이론단 높이의 증가를 막을 수 있다.
소용돌이 확산에 따른 사용한 컬럼의 계수로서 이동상의 속도와 관련없는 항목으로 아래 그림에서와 같이 분석시료가 다양한 경로로 진행함으로써 생긴다. 작고 균질한 입자를 사용하며, 균일한 충진을 하면 줄어들 수 있다.
B : longitudinal diffusion
세로확산에 따른 사용한 컬럼의 계수로서 이동상과 정 혹은 반대의 방향으로 생기는 확산을 말한다. 이동상의 유속과 반비례하므로이동상이 액체이면 확산은 약 10-5정도이므로 LC에서는 무시할 수 있으나 GC에 있어서는 carrier gas의 속도와 종류에 따라 영향을 미치게 된다.
C : mass transfer
질량이동에 따른 사용한 컬럼의 계수로서 평형의 불충분으로 인해서 생기는 항목으로정지상의 기하학적 구조, 분배계수 및 두 상에서의 확산속도 등의 영향을 받는다. 정지상의 두께(컬럼의 지름)를 얇게 하고 분리 온도를 높여 빠른 평형을 가능하게 하면 이를 줄일 수 있다. GC의 경우 film thickness가 작아지면 이 항목으로 인한 band broadening이 발생할 확률이 작아진다. 또한 유속을 낮추면 평형에 충분한 시간을 주게 되므로 이론단 높이의 증가를 막을 수 있다.
U : 이동상의 유속
van Deemter식에서 A, B, C 각 항의 HETP에 대한 기여도를 보여주는 HETP와 U의 곡선은 다음과 같다.
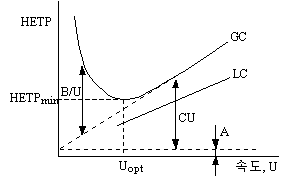
그림에서 LC의 경우 B항이 무시되므로 GC와 구분되는 것을 알 수 있다.
HETP를 최소화 할 수 있는 실험 조건은 아래와 같다.
- 정지상 입자의 크기는 작아야 한다.
- 이동상의 유속은 가능한 느려야 한다. (일반적으로 1.0ml/min을 많이 사용)
- 이동상의 점도는 작을수록 좋다. (0.5cp 이하)
- 컬럼의 온도는 높을수록 좋다.
- 작은 입자의 정지상이 충전된 긴 컬럼의 사용
- 시료 주입량은 적을수록 좋다.
- 분자량이 작은 시료일수록 분리가 용이하다. (일반적으로 1,000이하)
2. 컬럼 외의 용리띠의 퍼짐
크로마토그램의 피크가 퍼지는 요인은 시료주입 시스템, 컬럼 연결부 구조, 컬럼 외의 연결관의 부피, 검출기 셀의 부피 등 다양하다.
용리띠의 퍼짐은 시료량이 클수록 증가된다. 보통 용리띠의 퍼짐은 부피단위로 표시하여 크로마토그램에서 관찰된 용리띠의 퍼짐을 VW이라 하고 컬럼 내에서의 퍼짐을 VP, 컬럼 외의 조건에 의한 퍼짐을 Vec라 하면 아래와 같은 관계식으로 표현 할 수 있다.
(VW)2 = (VP)2 + (Vec)2
컬럼 내에서의 퍼짐을 기준으로 식을 정리하면,
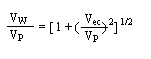
이것은 컬럼 내 퍼짐이 큰 경우는 컬럼 외에서 퍼짐이 일어나는 효과가 전체 용리띠의 퍼짐에 미치는 영향은 크지 않음을 의미한다. 따라서 아래와 같은 몇 가지 결과를 얻을 수 있다.
- N이 크고 HETP가 작은 컬럼일수록 컬럼의 퍼짐의 요건은 중요하다.
- 머무름이 길수록 tW와 VP가 커지므로 컬럼외 퍼짐의 요인은 빨리 용리되는 성분에 대해 그 영향이 크다.
- 컬럼의 내경이 크고 길이가 길수록 컬럼외 퍼짐 요인의 영향은 적어진다.
주입하는 시료는 일반적으로 처음 용리되는 성분의 VP보다 1/3보다는 적어야 된다. 일반적으로 LC의 VP는 약 100㎕보다 크므로 컬럼 외 퍼짐은 100㎕보다는 적은데 이상적인 값은 30㎕보다 적어야 한다.
연결관의 dimension에 기인한 퍼짐을 Vi이라 하면 아래와 같이 식으로 표현할 수 있다.
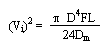 | L : 연결관의 길이 D : 내경 Dm : 이동상의 확산계수 |
머무름(Retention)에 미치는 시료 양의 영향
(1) 두 성분 시료의 경우
시료의 양이 많아질수록 머무름 시간의 감소가 일어나며 서로 피크가 겹치고 대칭성도 잃게 된다.
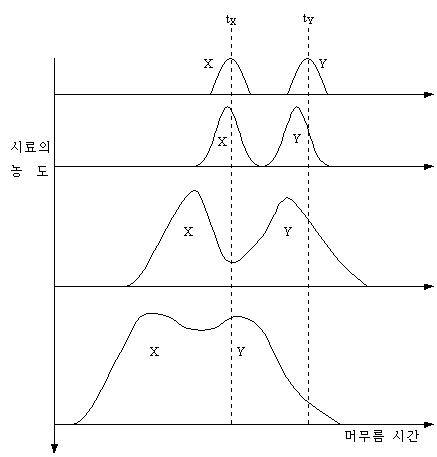
(2) 한가지 시료 경우를 통한 시료의 주입량
위의 경우에서 보듯이 컬럼의 분리능에 비해 과다한 양의 시료를 주입해서는 정확한 분리 및 분석결과를 얻기를 기대하기는 어렵다. 분석되는 시료의 양에 대한 영향을 정량적으로 알아보기 위해서는 정지상의 무게에 대한 시료의 무게를 고려해야 한다.
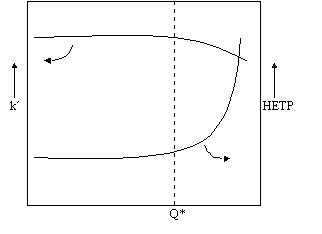
만약 이 정지상의 무게에 대한 시료의 무게비를 Q라 한다면 이 Q와 머무름 시간이나 k' 혹은 HETP)과의 관계를 그래프로 그리면 아래와 같다. Q가 낮은 범위에서는 머무름 시간이 일정하고 k'도 일정하며 피크의 대칭성과 퍼짐에 관여하는 HETP 역시 일정하다. 그러나 Q값이 어느 이상 커지게 되면 k'은 감소하게 되고 HETP는 증가하게 된다. 이러한 변화점에서의 Q를 Q*라 하면 이 점을 기준으로 이하인 점은 일반적으로 분석용 LC 즉, Analytical LC 이 이상의 점은 제조용 LC 즉, Preparative LC의 범위로 분류할 수 있다.
Column Efficiency - 이론단수 측정방법
이론단수(Theoretical Plate)는피크의형태와 상황에따라측정법이다양하다. 우선 피크가 아래 그림과 같은정규분포곡선 형태라면 N은다음과같이정의된다.
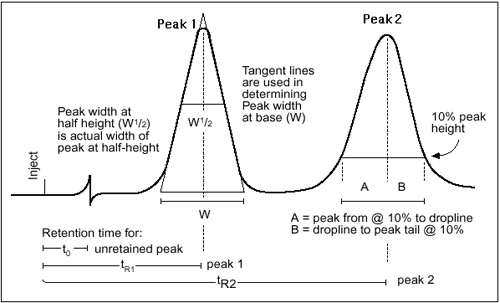
a : constant depending on method used
tr : retention time of peak
W : peak height
이 때 a, 즉 각 방법에 따른 상수는 아래와 같다.
W a Wi 4 Wh 5.54 W3 σ 9 W4σ 16 W5σ 25 Wtan 16
위의 방법 중에서 1/2 Peak Height법을 가장 많이 사용하며, 이를 적용하면 이론단수는 다음과 같다.
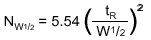
그러나 실제 분석에서 나타나는 피크의 형태는 가우스 곡선의 형태를 취하지 않으며 따라서 결과는 이론과 같지 못하다. 그렇다면각 방법의 특징을 알아보자.
① 변곡점법 (Inflection method)
이 방법은 정확도가 가장 낮다. 보통 피크는 이 높이에서 변곡점을 가지며 이 말은 피크의 형태가 아랫 부분에서 어떠한 형태 즉 앞끌기(fronting), 꼬리끌기(tailing)가 있어도 영향을 받지 않는다는 것이므로 피크의 형태에 탄력성없는 계산법이 되는 것이다.
② 반높이 너비법 (Half width method)
이 방법도 피크가 비대칭성이 되는 것에 있어 비대칭성의 영향을 받지 않는 방법이다. 하지만 이 방법은 측정자에 따라 값이 달라질 수 있는 오차를 줄일 수 있는 방법으로 결과 계산값에 대한 재현성이 크다.
③ 접선법 (Tangent method)
이것은 앞의 두 방법과 달리 피크의 형태에 따라 접선을 그어 계산하므로 비대칭성의 영향이 고려되는 방법이다. 하지만 이것은 측정자에 따라 접선을 긋는 것이 달라질 수가 있어 측정치의 편차가 있을 수 있다.
④ 3σ, 4σ, 5σ법
이 방법들은 피크의 비대칭성에 아주 직접적인 영향을 받아 결과에 반영한다. 이들 중 5σ법이 가장 예민한데 접선법과 비교시tailing이 있는 피크의 경우 접선법의 경우 9,000정도일 때 5σ법은 3,000정도 밖에 안된다.
⑤ 높이-면적비법 ( Height-area method)
가우스 분포곡선 봉우리의 면적(A)은 피크의 높이(h)와 표준편차(σt)의 함수가 된다.
A = (2π)1/2σt h
이 식은 σ에 대해 다시 정리하여 N에 대한 식으로 정리하면 아래와 같다.
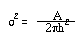
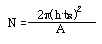
⑥ 모멘트 법 (Moment method)
먼저 모멘트 법에 의한 계산 수식은 아래와 같다.
여기서의 M1은 피크의 중심으로 무게중심에서 생긴다. 가우스 봉우리에서는 tR과 일치한다. 그러나 가우스의 곡선을 따르지 않는경우 피크의 중심은 조금씩 상이하게 될 것이다. 이것은 앞끌기나 꼬리 끌기가 되었을 경우 중심이 이동하는 것이고 이것은 이 시료의 농도의 중심 역시 이동하는 것으로 볼 수 있다. M2는 봉우리의 변화이고 5번의 수식을 따르면 된다.
방법은 기준 바탕선(baseline)에 잡음이 있을 경우 피크의 시작과 끝을 결정하는데에서 오차가 발생할 수 있다. 하지만 컴퓨터나 기타 장치를 동원한다면 가장 정확한 방법이 될 수 있다.
⑦ 비대칭 기준법
이 방법은 비대칭 피크의 비대칭비 (asymmetry ratio)를 구하여 계산하는 방법이다. 여기서는 이 비대칭비와 N을 계산하는 수식을소개하는 것으로 설명을 마치겠다.
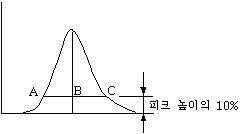
비대칭비를 T라 하면, T = BC/AB이다. 이것을 이용하여 Foley와 Dorsey가 N을 구하는 관계식을 유도하였는데 아래와 같다.
분해능 (Resolution : Rs)
한 성분이 서로 인접된 다른 성분과 어느 정도 정량적으로 분리되어 있는가를 표시하는 값을 말한다. 그래서 보통 상대적으로 N값이 크고 HETP의 값이 작은 컬럼을 통해서 분리되어 나온 시료의 크로마토그램은 분리도가 비교적 크다. 분리도는 크로마토그램을 통해 구할 수 있고 이것은 인접한 두 피크의 머무른 시간의 차이가 클수록 그리고 띠 폭의 평균값이 작을수록 커진다.
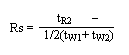
이 Rs와 분리되는 두 성분간의 농도비는 크로마토그램의 모양에 영향을 준다. 같은 Rs값을 가진다고 해도 농도비에 따라 아래의 그림과 같이 분리 양상이 달라진다. 그림에서 보는 것과 같이 Rs값이 작고 농도비가 클수록 분리가 모호해진다.
앞에서 말한 식에서 tR1 = (1+k1´)이고 tR2 = (1+k2´)이다. 그러므로 Rs = to (k2´- k1´)/ tW1 이 된다. 여기서 tW1는 이론단수를 구하는 수식에서 4to(1+k´) / N1/2 이므로 Rs에 대한 식은 아래와 같이 표기할 수 있다.
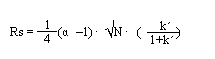
Rs는 위와 같은 식으로 각각의 파라미터를 계산하여 얻을 수 있다. 결국 좋은 분리 결과를 얻기 위해 이런 파라미터의 값들을 증대시키는 것은 Rs를 높이는 것과 같다. 위의 파라미터와 관련된 실험조건은 다음과 같다.
α : 주로 이동상 및 정지상의 조성
N : 주로 컬럼의 길이, 정지상의 입자크기, 이동상의 유속
k´ : 주로 이동상의 용매세기
N : 주로 컬럼의 길이, 정지상의 입자크기, 이동상의 유속
k´ : 주로 이동상의 용매세기
(1) 분리도(Rs)와 k´, N, α와의 관계
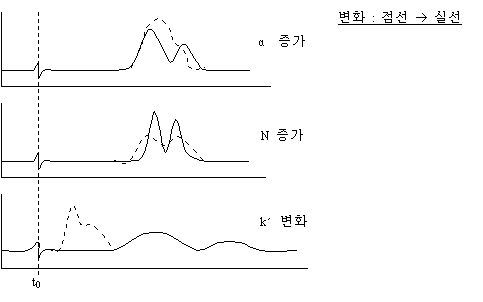
(2) Rs와 k´와의 관계
일반적으로 k´의 값에 Rs는 비례적으로 변화한다. k´의 영향은 k´가 작을 경우 (0≤k´≤1)는 크고, k´(1≤k´≤10)가 클 때는 분리도에 전혀 영향을 미치지 않는다. 앞에서 언급한 것처럼 k´의 변화는 시료, 정지상, 이동상의 3자 관계에 의해 결정된다. k´를 증가시키기 위해서는 약한 용매를 감소시키기 위해서는 강한 용매를 사용함으로써 가능하다.
(3) Rs와 N과의 관계
세가지 변수 중에서 영향이 크고 분리시간, 압력, 컬럼 길이와 상관관계를 가지므로 나머지 두 인자보다 체계적이다. 분리도를 증대시키기 위해 N을 증가시키는 방법은 아래의 3가지 방법이 있다.
- 컬럼 길이 고정 - 압력 감소
- 압력 고정 - 컬럼 길이 증가
- 분리 시간 고정 - 길이와 압력 증가
(4) Rs와 α의 관계
α가 증가되어 분리도가 증대되는 것은 N증가나 k´의 적당한 증가보다 더 효과적이다. α의 증가는 한 성분이 다른 성분으로부터 멀어지면서 분리시간은 감소되기 때문이다. 하지만 α값을 증가시키는 것은 실질적으로 어렵고 제시된 일정한 방법도 없다. α를 증가시키는 실험적인 방법은 다음과 같다.
- 이동상의 조성을 변화
- 이동상의 액성을 조절 (pH)
- 정지상을 적당한 것으로 바꾼다.
- 분리온도 조절
- 분리될 성분과의 화학반응 이용
(5) Rs와 그외의 인자의 관계
분리시간과 컬럼에 걸리는 압력 등이 있다. 압력이 증가하면 이론단수의 숫자가 늘어나 컬럼의 분리 효율성이 높아진다. 복잡한 수식은 여기서는 생략하겠다. 하지만 그런 수식들로 인해서 압력이 10배 증가하면 분리도가 2배가 증가되고 P가 일정할 때에는 이론단수의 수는 t0.7에 비례한다.
분리시간 (t = tR)
보통 분리시간이라 하면 시료가 주입되어 제일 마지막 성분이 분리도어 나오는 데까지 걸리는 시간을 의미한다. 만약 시료가 두 성분이라 한다면 그 식은 아래와 같다.
t = tR2 = to ( 1 + k2´)
일반적으로 LC에서 성분의 k´은 3~20정도이다. 즉 위 식에서의 tR2은 4to~20to정도가 됨을 의미한다. 따라서 분리시간은 to에 의존하는 것이다. 여기서는 간략히 말해서 t0를 좌우하는 인자들은 컬럼의 다공성(column porosity), 이동상의 점도(viscosity), 컬럼의 길이 및 컬럼에 걸리는 압력이다.
출처 : https://blog.naver.com/nanomate/110003143460
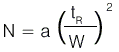
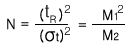
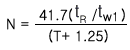
댓글 없음:
댓글 쓰기