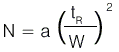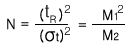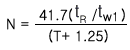자유롭게 커스토마이징할 수 있다는 강력한 장점이 있지만
HTML을 적극적으로 활용하지 않는 입장에서는 그저
여러 기능의 부재를 직접 끼워맞춰 추가해 사용해야 하는 부담감이 남아있을 뿐이다.
장점 : Google이 호스팅하는 24/7 uptime을 보여주는 안정성
단점 : 알려주지 않으면 아무것도 할 줄 모름.
2018-11-22
리눅스(CentOS)의 마우스와 키보드가 먹통됐다.
오랜 연산이 필요한 작업을 terminal에서 진행시켜둔 다음
Ctrl + Alt + ↓, ↑로 와리가리(?)를 좀 했더니
갑자기 컴퓨터가 띵깡을 부리기 시작했다.
마우스를 움직이는 것이 가능하고, Ctrl + Alt + F2를 눌러서 tty2로 진입이 가능했다.
게다가 연산중이던 프로세스는 정상 가동중이다.
근데 마우스는 i beam cursor 모양으로 계속 움직여진다.
이게 무슨 상황인지 모르겠다.
python formatting
for i in range(5):
i=i+1
print("{0:0>10}".format(i))
print("="*30)
print("{0:=>10}".format(i))
print("{0:=<10 format="" i="" p="">print("{0:=^10}".format(i))
print("{0:=>10}".format(i))
0000000001
0000000002
0000000003
0000000004
0000000005
==============================
=========5
5=========
====5=====
=========5
<10 format="" i="" p="">
참조하기 좋은 곳
한자키 없이 특수문자 치기 : 알트 입력법(ALT CODE)
그러고보니 의구심이 들었다.
외국인들은 '한자키'없이 어떻게 특수문자들을 편리하게 쳐왔을까?
이는 이미 옛날부터 존재해온 방식이 있었다.
알트 입력법(Alt code)이란 방식이 있다.
이는 IBM PC에서 최초로 사용한 방식이라고 한다.
알트 키를 누른 채로 십진법으로 숫자를 입력하면
시스템 바이오스는 대응하는 코드를 키보드 버퍼에 넣는다.
이렇게 바이오스를 통해 문자를 입력받는 소프트웨어 입장에서는
특정 키를 하나 띡 눌러서 입력된 것처럼 인식하게 된다.
사용법은 위에서 말한대로
알트 키를 누른 채, 문자에 해당하는 값을 누른 뒤, 알트 키에서 손을 떼면 된다.
반드시 키보드 오른쪽의 숫자 키패드를 사용해서 입력해야 한다.
예를 들어서 Alt + 133은 … 이라고 타이핑되며, Alt + 189는 ½ 라고 타이핑된다.
원하는 기호가 어떤 코드인지는
엑셀에서 =CODE("ð") 처럼 입력해보면 값을 알 수 있다.
2018-11-07
script
# MMPBSA.py -O -i mmpbsa.in -o FINAL_RESULTS_MMPBSA.dat -sp comp0.prmtop -cp compx0.top -rp protein0.top -lp lig0.top -y 04Produ.mdcrd
for i in range(1, 16):
num = str(i)
print("mkdir comp%d" % i) # make directory
print("cp mmpbsa.in ./comp%d/mmpbsa.in" % i) # mmpbsa.in
print("mv comp%d.prmtop ./comp%d/comp%d.prmtop" % (i, i, i)) # comp
print("mv compx%d.prmtop ./comp%d/compx%d.prmtop" % (i, i, i)) # compx
print("mv protein%d.prmtop ./comp%d/protein%d.prmtop" % (i, i, i)) # protein
print("mv lig%d.prmtop ./comp%d/lig%d.prmtop" % (i, i, i)) # ligand
print("mv 04Produ%d.mdcrd ./comp%d/04Produ%d.mdcrd" % (i, i, i)) # trajectory
print("cd comp%d/" % i) # go into the folder
print("MMPBSA.py -O -i mmpbsa.in -o RESULT%d.dat "
"-sp comp%d.prmtop "
"-cp compx%d.top "
"-rp protein%d.top "
"-lp lig%d.top "
"-y 04Produ.mdcrd" % (i, i, i, i, i)) # running MMPBSA
print("cd ..") # exit folder
print("")
# mkdir comp1
# cp mmpbsa.in ./comp1/mmpbsa.in
# mv comp1.prmtop ./comp1/comp1.prmtop
# mv compx1.top ./test/compx0.top
# mv protein0.top ./test/protein0.top
# mv lig0.top ./test/lig0.top
# mv 04Produ.mdcrd ./test/04Produ.mdcrd
# cd test/
# MMPBSA.py -O -i mmpbsa.in -o FINAL_RESULTS_MMPBSA.dat -sp comp0.prmtop -cp compx0.prmtop -rp protein0.top -lp lig0.top -y 04Produ.mdcrd
# cd ..
# blank line
2018-11-01
HPLC Separation Theory
HPLC 컬럼은 튜빙 내에 입자크기가 5~10 ㎛인 충진물질(Stationary Phase)을 채워서 사용한다. 충진물질은 분리하고자 하는 물질에 따라 다양한 물질을 사용하며, 세부적인 내용은 2장을 참조하기 바란다. 튜빙은 600 psi보다 낮은 압력에서 유리관을 사용하기도 하지만 일반적으로 Stainlessless Steel로 만들어진다. 대부분의 HPLC 컬럼은 10~30 cm이며 내부 지금은 4~10 cm이다. 이 형태의 컬럼은 대개 40,000~60,000 이론단수/m를 가진다. 최근에는 내부지름이 1~4.6 mm 이고 이론단수가 100,000에 이르는 마이크로 컬럼을 사용하기도 한다.
HPLC 컬럼에서 용리가 일어나는 동안 한 개의 용질 분자가 정지상과 이동상 사이에서 수많은 이동이 일어난다. 각 상에서 머무르는 시간은 아주 불규칙적이다. 한 상에서 다른 상으로의 이동은 에너지를 필요로 하는데 분자는 이 에너지를 주위에서 얻어야 한다. 따라서 어떤 분자는 주어진 상에서 머무르는 시간이 순간적이고, 어떤 분자는 머루르는 시간이 상대적으로 길 수도 있다. 컬럼 속에서 이동은 분자가 이동상 내에 있을 때에만 일어나며, 결과적으로 시료를 구성하고 있는 성분들의 이동속도는 그들이 정지상에 머무르는 시간에 따라 달라진다. 이들의 이동속도는 일반적으로 평균이동속도를 중심으로 대칭으로 퍼진 Gaussian Peak의 형태를 띠게 된다.
시료의 분리-용리띠의 퍼짐
1. 컬럼에서의 용리띠 퍼짐
컬럼에서 발생하는 퍼짐을 설명하는 주요한 두 가지 이론은 단이론(Plate theory)과 속도이론(Rate theory)이다.
(1) 단이론(Plate theory)
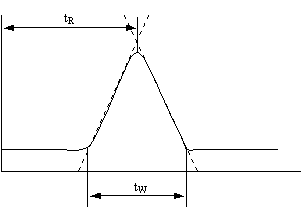
단이란 이론상의 단으로 컬럼의 내부가 수많은 크기가 동일한 분리층으로 구성되어 있다고 가정한다. 이러한 단에서는 최소한의 시료들의 분리가 일어나며, 단 수가 많다면 분리가 많이 일어나서 결과가 좋을 것이다. 이렇게 컬럼 내의 분리에 관여하는 단의 수를 이론단수(Number of theoretical plates, N)라 한다. N은 띠폭(band width)를 tW로 하고 피크가 기준선(혹은 바탕선:baseline)과 만나는 지점의 사이를 측정하여 얻는다. 이렇게 해서 가우스 분포곡선을 용리띠로 생각해서 수학적으로 근사한 관계를 얻을 수 있다.
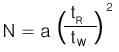 | a : constant depending on method used tR : retention time of peak tW : peak width |
동일한 조건(컬럼과 이동상, 유속, 온도, 시료 주입방법 등)에서는 크로마토그램의 어느 성분의 피크로부터 N값을 계산하든지 거의 일정한 값을 보이게 된다. 일반적으로 컬럼의 효율(Column efficiency)을 N값으로 표현하고 이러한 N값이 클수록 분리능은 높아지게 된다. 이러한 분리를 잘되게 하는 N을 증가시키는 방법에는 두가지가 있다.
① 컬럼의 길이 증가
컬럼의 단은 동일하고 일정한 간격을 가지고 있으므로 컬럼의 길이(L)를 증가하면 N은 증가한다. 하지만 길이를 증가시키면 tR과 tW도 따라서 증가하게 된다. 이 때 각각의 값들이 증가하는 정도를 보면 길이가 2배로 늘어났을 때 tR = L/U(1+ k')에서 알 수 있듯이 2배로 증가한다. 따라서 tW는 21/2배 증가하게 된다.
컬럼의 단은 동일하고 일정한 간격을 가지고 있으므로 컬럼의 길이(L)를 증가하면 N은 증가한다. 하지만 길이를 증가시키면 tR과 tW도 따라서 증가하게 된다. 이 때 각각의 값들이 증가하는 정도를 보면 길이가 2배로 늘어났을 때 tR = L/U(1+ k')에서 알 수 있듯이 2배로 증가한다. 따라서 tW는 21/2배 증가하게 된다.
② 정지상 입자의 크기를 감소 일반적으로 사용자가 입자의 크기를 감소할 수는 없고 더 작은 입자로 구성된 컬럼을 구입하여 사용하는 방법인데 이 경우 머무름 시간을 증가시키지 않고 N값을 증가시키는 방법이다. 컬럼길이를 증가하는 것보다는 효과적이다. 상품의 사양에 입자의 크기가 나오기는 하지만 이론적으로 입자의 크기는 컬럼의 길이를 N값으로 나눈 것이다. 이것을 이론단 해당높이(HETP : Height Equivalent to a Theoretical Plate)라고 부른다. 다시 말해서 HETP를 식으로 나타내면
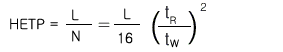
와 같다. 이 방법은 결국 HETP를 줄이는 결과를 가져오는데 이 방법은 길이(L)가 고정되고 tR은 증가되지 않으므로 결국에는 tW이 감소되어 좁은 피크를 얻게 되어 좋은 분리 결과를 가져오게 된다.
2) 속도이론(Rate theory)
HETP값이 이상적인 경우 0값을 보이지만 실제는 항상 시료들이 퍼짐현상을 보이게 되고 결국은 HETP 값은 항상 0보다 크게 되는 것에 관련하여 생각하는 것이다. 이러한 퍼짐현상은 앞에서 설명한 소용돌이 확산, 세로확산, 질량이동 현상의 3가지로 간단히 규정하고 HETP와의 관계를 식으로 보면 아래와 같다.
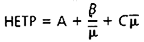
이 식은 네덜란드의 석유화학자 그룹이 수학적으로 유도한 것으로 van Deemter식이라 부른다. 이 식에서 HETP를 증가시키는 방법은 A항을 작게 B, C항은 적당한 유속으로 B와 C항의 합이 최소가 되도록 하여야 한다.
A : eddy diffusion
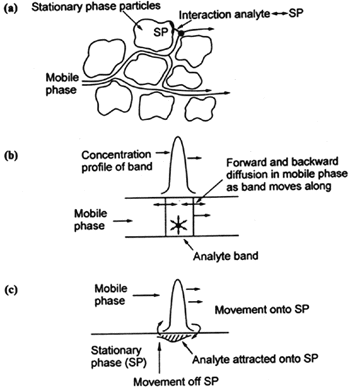
소용돌이 확산에 따른 사용한 컬럼의 계수로서 이동상의 속도와 관련없는 항목으로 아래 그림에서와 같이 분석시료가 다양한 경로로 진행함으로써 생긴다. 작고 균질한 입자를 사용하며, 균일한 충진을 하면 줄어들 수 있다.
B : longitudinal diffusion
세로확산에 따른 사용한 컬럼의 계수로서 이동상과 정 혹은 반대의 방향으로 생기는 확산을 말한다. 이동상의 유속과 반비례하므로이동상이 액체이면 확산은 약 10-5정도이므로 LC에서는 무시할 수 있으나 GC에 있어서는 carrier gas의 속도와 종류에 따라 영향을 미치게 된다.
C : mass transfer
질량이동에 따른 사용한 컬럼의 계수로서 평형의 불충분으로 인해서 생기는 항목으로정지상의 기하학적 구조, 분배계수 및 두 상에서의 확산속도 등의 영향을 받는다. 정지상의 두께(컬럼의 지름)를 얇게 하고 분리 온도를 높여 빠른 평형을 가능하게 하면 이를 줄일 수 있다. GC의 경우 film thickness가 작아지면 이 항목으로 인한 band broadening이 발생할 확률이 작아진다. 또한 유속을 낮추면 평형에 충분한 시간을 주게 되므로 이론단 높이의 증가를 막을 수 있다.
소용돌이 확산에 따른 사용한 컬럼의 계수로서 이동상의 속도와 관련없는 항목으로 아래 그림에서와 같이 분석시료가 다양한 경로로 진행함으로써 생긴다. 작고 균질한 입자를 사용하며, 균일한 충진을 하면 줄어들 수 있다.
B : longitudinal diffusion
세로확산에 따른 사용한 컬럼의 계수로서 이동상과 정 혹은 반대의 방향으로 생기는 확산을 말한다. 이동상의 유속과 반비례하므로이동상이 액체이면 확산은 약 10-5정도이므로 LC에서는 무시할 수 있으나 GC에 있어서는 carrier gas의 속도와 종류에 따라 영향을 미치게 된다.
C : mass transfer
질량이동에 따른 사용한 컬럼의 계수로서 평형의 불충분으로 인해서 생기는 항목으로정지상의 기하학적 구조, 분배계수 및 두 상에서의 확산속도 등의 영향을 받는다. 정지상의 두께(컬럼의 지름)를 얇게 하고 분리 온도를 높여 빠른 평형을 가능하게 하면 이를 줄일 수 있다. GC의 경우 film thickness가 작아지면 이 항목으로 인한 band broadening이 발생할 확률이 작아진다. 또한 유속을 낮추면 평형에 충분한 시간을 주게 되므로 이론단 높이의 증가를 막을 수 있다.
U : 이동상의 유속
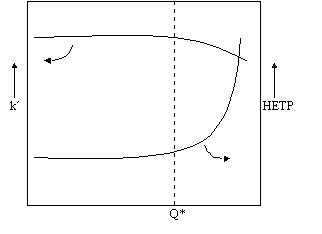
van Deemter식에서 A, B, C 각 항의 HETP에 대한 기여도를 보여주는 HETP와 U의 곡선은 다음과 같다.
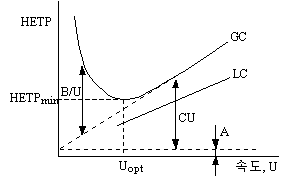
그림에서 LC의 경우 B항이 무시되므로 GC와 구분되는 것을 알 수 있다.
HETP를 최소화 할 수 있는 실험 조건은 아래와 같다.
- 정지상 입자의 크기는 작아야 한다.
- 이동상의 유속은 가능한 느려야 한다. (일반적으로 1.0ml/min을 많이 사용)
- 이동상의 점도는 작을수록 좋다. (0.5cp 이하)
- 컬럼의 온도는 높을수록 좋다.
- 작은 입자의 정지상이 충전된 긴 컬럼의 사용
- 시료 주입량은 적을수록 좋다.
- 분자량이 작은 시료일수록 분리가 용이하다. (일반적으로 1,000이하)
2. 컬럼 외의 용리띠의 퍼짐
크로마토그램의 피크가 퍼지는 요인은 시료주입 시스템, 컬럼 연결부 구조, 컬럼 외의 연결관의 부피, 검출기 셀의 부피 등 다양하다.
용리띠의 퍼짐은 시료량이 클수록 증가된다. 보통 용리띠의 퍼짐은 부피단위로 표시하여 크로마토그램에서 관찰된 용리띠의 퍼짐을 VW이라 하고 컬럼 내에서의 퍼짐을 VP, 컬럼 외의 조건에 의한 퍼짐을 Vec라 하면 아래와 같은 관계식으로 표현 할 수 있다.
(VW)2 = (VP)2 + (Vec)2
컬럼 내에서의 퍼짐을 기준으로 식을 정리하면,
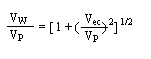
이것은 컬럼 내 퍼짐이 큰 경우는 컬럼 외에서 퍼짐이 일어나는 효과가 전체 용리띠의 퍼짐에 미치는 영향은 크지 않음을 의미한다. 따라서 아래와 같은 몇 가지 결과를 얻을 수 있다.
- N이 크고 HETP가 작은 컬럼일수록 컬럼의 퍼짐의 요건은 중요하다.
- 머무름이 길수록 tW와 VP가 커지므로 컬럼외 퍼짐의 요인은 빨리 용리되는 성분에 대해 그 영향이 크다.
- 컬럼의 내경이 크고 길이가 길수록 컬럼외 퍼짐 요인의 영향은 적어진다.
주입하는 시료는 일반적으로 처음 용리되는 성분의 VP보다 1/3보다는 적어야 된다. 일반적으로 LC의 VP는 약 100㎕보다 크므로 컬럼 외 퍼짐은 100㎕보다는 적은데 이상적인 값은 30㎕보다 적어야 한다.
연결관의 dimension에 기인한 퍼짐을 Vi이라 하면 아래와 같이 식으로 표현할 수 있다.
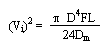 | L : 연결관의 길이 D : 내경 Dm : 이동상의 확산계수 |
머무름(Retention)에 미치는 시료 양의 영향
(1) 두 성분 시료의 경우
시료의 양이 많아질수록 머무름 시간의 감소가 일어나며 서로 피크가 겹치고 대칭성도 잃게 된다.
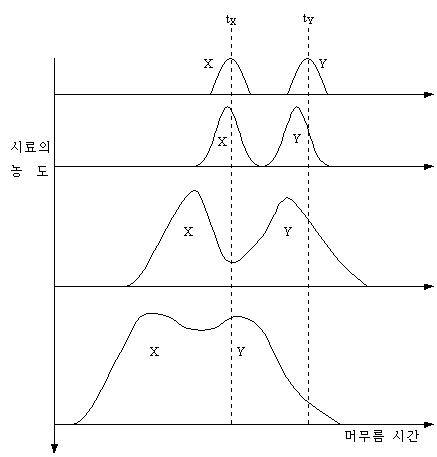
(2) 한가지 시료 경우를 통한 시료의 주입량
위의 경우에서 보듯이 컬럼의 분리능에 비해 과다한 양의 시료를 주입해서는 정확한 분리 및 분석결과를 얻기를 기대하기는 어렵다. 분석되는 시료의 양에 대한 영향을 정량적으로 알아보기 위해서는 정지상의 무게에 대한 시료의 무게를 고려해야 한다.
만약 이 정지상의 무게에 대한 시료의 무게비를 Q라 한다면 이 Q와 머무름 시간이나 k' 혹은 HETP)과의 관계를 그래프로 그리면 아래와 같다. Q가 낮은 범위에서는 머무름 시간이 일정하고 k'도 일정하며 피크의 대칭성과 퍼짐에 관여하는 HETP 역시 일정하다. 그러나 Q값이 어느 이상 커지게 되면 k'은 감소하게 되고 HETP는 증가하게 된다. 이러한 변화점에서의 Q를 Q*라 하면 이 점을 기준으로 이하인 점은 일반적으로 분석용 LC 즉, Analytical LC 이 이상의 점은 제조용 LC 즉, Preparative LC의 범위로 분류할 수 있다.
Column Efficiency - 이론단수 측정방법
이론단수(Theoretical Plate)는피크의형태와 상황에따라측정법이다양하다. 우선 피크가 아래 그림과 같은정규분포곡선 형태라면 N은다음과같이정의된다.
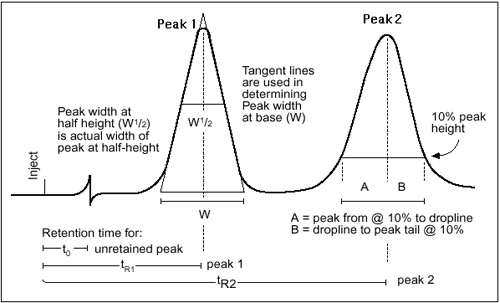
a : constant depending on method used
tr : retention time of peak
W : peak height
이 때 a, 즉 각 방법에 따른 상수는 아래와 같다.
W a Wi 4 Wh 5.54 W3 σ 9 W4σ 16 W5σ 25 Wtan 16
위의 방법 중에서 1/2 Peak Height법을 가장 많이 사용하며, 이를 적용하면 이론단수는 다음과 같다.
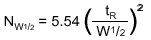
그러나 실제 분석에서 나타나는 피크의 형태는 가우스 곡선의 형태를 취하지 않으며 따라서 결과는 이론과 같지 못하다. 그렇다면각 방법의 특징을 알아보자.
① 변곡점법 (Inflection method)
이 방법은 정확도가 가장 낮다. 보통 피크는 이 높이에서 변곡점을 가지며 이 말은 피크의 형태가 아랫 부분에서 어떠한 형태 즉 앞끌기(fronting), 꼬리끌기(tailing)가 있어도 영향을 받지 않는다는 것이므로 피크의 형태에 탄력성없는 계산법이 되는 것이다.
② 반높이 너비법 (Half width method)
이 방법도 피크가 비대칭성이 되는 것에 있어 비대칭성의 영향을 받지 않는 방법이다. 하지만 이 방법은 측정자에 따라 값이 달라질 수 있는 오차를 줄일 수 있는 방법으로 결과 계산값에 대한 재현성이 크다.
③ 접선법 (Tangent method)
이것은 앞의 두 방법과 달리 피크의 형태에 따라 접선을 그어 계산하므로 비대칭성의 영향이 고려되는 방법이다. 하지만 이것은 측정자에 따라 접선을 긋는 것이 달라질 수가 있어 측정치의 편차가 있을 수 있다.
④ 3σ, 4σ, 5σ법
이 방법들은 피크의 비대칭성에 아주 직접적인 영향을 받아 결과에 반영한다. 이들 중 5σ법이 가장 예민한데 접선법과 비교시tailing이 있는 피크의 경우 접선법의 경우 9,000정도일 때 5σ법은 3,000정도 밖에 안된다.
⑤ 높이-면적비법 ( Height-area method)
가우스 분포곡선 봉우리의 면적(A)은 피크의 높이(h)와 표준편차(σt)의 함수가 된다.
A = (2π)1/2σt h
이 식은 σ에 대해 다시 정리하여 N에 대한 식으로 정리하면 아래와 같다.
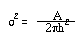
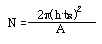
⑥ 모멘트 법 (Moment method)
먼저 모멘트 법에 의한 계산 수식은 아래와 같다.
여기서의 M1은 피크의 중심으로 무게중심에서 생긴다. 가우스 봉우리에서는 tR과 일치한다. 그러나 가우스의 곡선을 따르지 않는경우 피크의 중심은 조금씩 상이하게 될 것이다. 이것은 앞끌기나 꼬리 끌기가 되었을 경우 중심이 이동하는 것이고 이것은 이 시료의 농도의 중심 역시 이동하는 것으로 볼 수 있다. M2는 봉우리의 변화이고 5번의 수식을 따르면 된다.
방법은 기준 바탕선(baseline)에 잡음이 있을 경우 피크의 시작과 끝을 결정하는데에서 오차가 발생할 수 있다. 하지만 컴퓨터나 기타 장치를 동원한다면 가장 정확한 방법이 될 수 있다.
⑦ 비대칭 기준법
이 방법은 비대칭 피크의 비대칭비 (asymmetry ratio)를 구하여 계산하는 방법이다. 여기서는 이 비대칭비와 N을 계산하는 수식을소개하는 것으로 설명을 마치겠다.
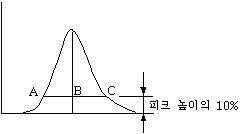
비대칭비를 T라 하면, T = BC/AB이다. 이것을 이용하여 Foley와 Dorsey가 N을 구하는 관계식을 유도하였는데 아래와 같다.
분해능 (Resolution : Rs)
한 성분이 서로 인접된 다른 성분과 어느 정도 정량적으로 분리되어 있는가를 표시하는 값을 말한다. 그래서 보통 상대적으로 N값이 크고 HETP의 값이 작은 컬럼을 통해서 분리되어 나온 시료의 크로마토그램은 분리도가 비교적 크다. 분리도는 크로마토그램을 통해 구할 수 있고 이것은 인접한 두 피크의 머무른 시간의 차이가 클수록 그리고 띠 폭의 평균값이 작을수록 커진다.
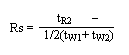
이 Rs와 분리되는 두 성분간의 농도비는 크로마토그램의 모양에 영향을 준다. 같은 Rs값을 가진다고 해도 농도비에 따라 아래의 그림과 같이 분리 양상이 달라진다. 그림에서 보는 것과 같이 Rs값이 작고 농도비가 클수록 분리가 모호해진다.
앞에서 말한 식에서 tR1 = (1+k1´)이고 tR2 = (1+k2´)이다. 그러므로 Rs = to (k2´- k1´)/ tW1 이 된다. 여기서 tW1는 이론단수를 구하는 수식에서 4to(1+k´) / N1/2 이므로 Rs에 대한 식은 아래와 같이 표기할 수 있다.
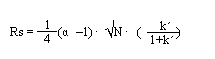
Rs는 위와 같은 식으로 각각의 파라미터를 계산하여 얻을 수 있다. 결국 좋은 분리 결과를 얻기 위해 이런 파라미터의 값들을 증대시키는 것은 Rs를 높이는 것과 같다. 위의 파라미터와 관련된 실험조건은 다음과 같다.
α : 주로 이동상 및 정지상의 조성
N : 주로 컬럼의 길이, 정지상의 입자크기, 이동상의 유속
k´ : 주로 이동상의 용매세기
N : 주로 컬럼의 길이, 정지상의 입자크기, 이동상의 유속
k´ : 주로 이동상의 용매세기
(1) 분리도(Rs)와 k´, N, α와의 관계
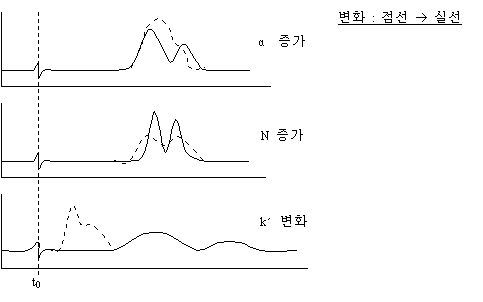
(2) Rs와 k´와의 관계
일반적으로 k´의 값에 Rs는 비례적으로 변화한다. k´의 영향은 k´가 작을 경우 (0≤k´≤1)는 크고, k´(1≤k´≤10)가 클 때는 분리도에 전혀 영향을 미치지 않는다. 앞에서 언급한 것처럼 k´의 변화는 시료, 정지상, 이동상의 3자 관계에 의해 결정된다. k´를 증가시키기 위해서는 약한 용매를 감소시키기 위해서는 강한 용매를 사용함으로써 가능하다.
(3) Rs와 N과의 관계
세가지 변수 중에서 영향이 크고 분리시간, 압력, 컬럼 길이와 상관관계를 가지므로 나머지 두 인자보다 체계적이다. 분리도를 증대시키기 위해 N을 증가시키는 방법은 아래의 3가지 방법이 있다.
- 컬럼 길이 고정 - 압력 감소
- 압력 고정 - 컬럼 길이 증가
- 분리 시간 고정 - 길이와 압력 증가
(4) Rs와 α의 관계
α가 증가되어 분리도가 증대되는 것은 N증가나 k´의 적당한 증가보다 더 효과적이다. α의 증가는 한 성분이 다른 성분으로부터 멀어지면서 분리시간은 감소되기 때문이다. 하지만 α값을 증가시키는 것은 실질적으로 어렵고 제시된 일정한 방법도 없다. α를 증가시키는 실험적인 방법은 다음과 같다.
- 이동상의 조성을 변화
- 이동상의 액성을 조절 (pH)
- 정지상을 적당한 것으로 바꾼다.
- 분리온도 조절
- 분리될 성분과의 화학반응 이용
(5) Rs와 그외의 인자의 관계
분리시간과 컬럼에 걸리는 압력 등이 있다. 압력이 증가하면 이론단수의 숫자가 늘어나 컬럼의 분리 효율성이 높아진다. 복잡한 수식은 여기서는 생략하겠다. 하지만 그런 수식들로 인해서 압력이 10배 증가하면 분리도가 2배가 증가되고 P가 일정할 때에는 이론단수의 수는 t0.7에 비례한다.
분리시간 (t = tR)
보통 분리시간이라 하면 시료가 주입되어 제일 마지막 성분이 분리도어 나오는 데까지 걸리는 시간을 의미한다. 만약 시료가 두 성분이라 한다면 그 식은 아래와 같다.
t = tR2 = to ( 1 + k2´)
일반적으로 LC에서 성분의 k´은 3~20정도이다. 즉 위 식에서의 tR2은 4to~20to정도가 됨을 의미한다. 따라서 분리시간은 to에 의존하는 것이다. 여기서는 간략히 말해서 t0를 좌우하는 인자들은 컬럼의 다공성(column porosity), 이동상의 점도(viscosity), 컬럼의 길이 및 컬럼에 걸리는 압력이다.
출처 : https://blog.naver.com/nanomate/110003143460
그러면 FID (Flame Ionization Detector)는 원리가 뭘까
TCD에 대해선 대강 개념을 이해했다.
양심없는 가격, 라이터 주제에
그렇다면 GC의 detector로 쓰이는 FID는 무엇이며, 왜 그걸 쓰고 있을까?
Flame Ionization Detector의 구조
FID의 구조는 위와 같다.
아래는 column으로부터 시료와 carrier gas가 나올 것이다. 다른 점이라면
air와 H_2 gas가 추가된 점인데, 이는 불꽃을 유지하기 위해 사용된다.
그렇게 column을 통과해 나온걸 불로 태워버리는데, 그 위엔 collector가 위치하고 있다.
이 collector와 불꽃 아래에는 약 300볼트 정도의 전기가 흐르고 있고,
시료가 불타면서 생기는 전기적 변화로 인해 이 전기적인 흐름에 변화가 생긴다.
대개 10^-9 에서 10^-12 암페어(amps) 정도의 변화가 생긴다.
이걸 증폭시킨 값이 대개 분석 신호로 쓰이곤 한다.
TCD보다도 FID를 사용하는 이유는 단연 '민감도' 때문이다.
FID의 검출한도는 최소 TCD보다 2~3배는 작은데다가,
10^6~10^7배 정도의 시료 주입량에도 선형적으로 반응해주는 등
넓은 스펙트럼의 성능을 자랑하고 있다.
GC 관리법 영상을 구경해보도록 하자. FID가 GC의 핵심 부품이다보니
조심스럽게 다뤄야 할 것 같다.
Anisotropy는 '비등방성'
비등방성은 위키에서 이렇게 설명하고 있다.
"비등방성(非等方性)(anisotropy)은 방향에 따라 물체의 물리적 성질이 다른 것을 말한다. 예를 들어, 솔질이 된 알루미늄, 섬유, 옷감, 근육 등의 표면은 들어오는 빛의 방향에 따라 반사율이 다른 광학적 비등방성을 띈다."
솔직히 뭔소린지 모르겠다. 그래서 이미지를 찾아보았다.
일단 '등방성(isotropy)'이란 말부터 이해해야 했다.
등방성이란 '물체의 물리적 성질이 방향에 따라 달라지지 않는 일'을 말한다고 한다.
즉, 어느 방향에서 쳐다보든 상관없이 물체의 물리적 성질은 똑같이 보인단 소리다.
비등방성의 대표적으로 지폐의 표면에 붙은 홀로그램이 있다.
보는 각도에 따라 다른 성질을 보이고 있는 것이 '비등방성(anisotropy)'이라는 뜻이다.
영문위키에서도 아래와 같이 설명하고 있다.
"Anisotropy /ˌænɪˈsɒtrəpi/, /ˌænaɪˈsɒtrəpi/ is the property of being directionally dependent, which implies different properties in different directions, as opposed to isotropy. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties (absorbance, refractive index, conductivity, tensile strength, etc.)"
비등방성은 굴절률이나 conductivity등의 예도 들 수 있다는데,
알고 싶었던 부분이 바로 이 부분이었다.
Gas chromatography에서 흔히 사용됐었던 detector로
TCD (Thermal Conductivity)라는게 있었다.
TCD는 두 개의 평행한 튜브가 가스를 운반하고, 코일에 의해 가열되는 구조라고 한다.
이렇게 생겼다.
왼쪽 관으로 reference column으로부터 나온 pure carrier gas가 흘러가고
오른쪽 관으론 analytic column에서 온 sample + carrier gas가 흐른다.
그리고 두 관에서 나온 가스들을 코일로 가열시켜서 heat loss rate를 측정한다.
두 관에서 온 가스의 열전도율이 다르다는 점에서 착안,
그 미묘한 차이를 측정한다는 원리로 탄생한 detector가 바로 TCD이다.
같은 문서에서 부가 설명하길
대부분 화합물들은 일반적으로 사용되는 hydrogen이나 helium같은 carrier gas들에 비해
conductivity가 훨씬 낮다고 한다.
그러니까 시료가 들어있는 column에서 온 gas의 conductivity가 훨씬 낮을테니
그 차이를 전기적으로 측정하면 되는 것이다.
그래서 conductivity에 있어서 anisotropy라는건 무엇을 뜻하는걸까?
그래서 다시 찾아보았다. Isotropic/anisotropic thermal conductivity는 무엇이 다른걸까..
아래와 같은 답변은 찾을 수 있었다.
""Anisotropic" means the thermal conductivity of the material depends on the direction the heat flows through the material. It can also cause strange behaviour where the heat does not flow in the same direction as the temperature gradient. Most common materials are isotropic. If your material data doesn't include anisotropic thermal properties, just ignore the option."
비등방성이란건 물질의 열전도율이 열이 흐르는 방향에 의존적이게 나타난다는 뜻입니다. 열이 높은 곳에서 낮은 곳으로 이동하는 구배에 따라 흐르지 않을 때 발생할 수 있습니다. 대부분의 물질은 등방성을 띱니다. 당신의 물질 데이터가 비등방성 열전도의 속성을 보이거든, 옵션을 무시하세요
옵션(?)이 뭔진 모르겠지만, 열이 이동함에 있어서
항상 고온에서 저온으로 이동하지만은 않는단걸 얘기하는 듯하다.
열의 이동도 하나의 '방향'으로 생각할 수 있다. 그런데 그 열의 이동방향에 따라
물질의 열전도율이 다르게 측정된다는 점이 anisotropic의 개념인 듯하다.
정확하게는 뭔소린가 잘 모르겠다 솔직히는...
그래서 더 찾아보았다. 완전하게 이해가 갈 때까지 찾아보려 한다.
다른 사이트를 참조했다.
열이 고온에서 저온으로 이동하며 평형을 이루게 됨은 누구나 아는 사실이다.
한편 열전도율은 온도 경사에 따른 열의 흐름 속성을 나타내는 말이다.
J는 열 흐름, k는 열전도율, dT/dr은 온도 구배이다.
석영에서 c축과 수직인 경우엔 conductivity가 6.5 Wm^-1K^-1이다.
하지만 c축과 평행할 때에는 11.3 Wm^-1K^-1까지 상승한다.
아하! 이 화합물은 방향에 따라 열전도율이 달라졌다.
그걸 어떻게 측정했을까 보았더니 이렇게 측정했다고 한다.
석영 크리스탈을 c 축과 수직으로 하나 자르고, 평행하게 하나 더 잘라놓는다.
두 조각을 수직으로 배치하고, 가운데에 열원을 둔다.
철을 데우면 가운데서부터 열을 받아서 전도되는 모습을 볼 수 있다.
동영상 참조
"방향에 따라 열전도율의 차이가 생긴다"라는 것이
heat conductivity에 있어서의 anisotropy의 개념이다.
이 개념으로 TCD의 사진을 다시 한 번 보면 조금 더 이해가 된다.

열 전도율이 다를테니 아래로부터(혹은 위로부터) 반대방향으로 열이 전달될 때
carrier gas보다 sampl + carrier gas의 열전도율이 낮을 것이다.
그 다른 정도를 옆의 detector가 전류의 흐름을 감지해서 구분해낸다.
이제야 이 사진이 전부 이해되었다.
"비등방성(非等方性)(anisotropy)은 방향에 따라 물체의 물리적 성질이 다른 것을 말한다. 예를 들어, 솔질이 된 알루미늄, 섬유, 옷감, 근육 등의 표면은 들어오는 빛의 방향에 따라 반사율이 다른 광학적 비등방성을 띈다."
솔직히 뭔소린지 모르겠다. 그래서 이미지를 찾아보았다.
일단 '등방성(isotropy)'이란 말부터 이해해야 했다.
등방성이란 '물체의 물리적 성질이 방향에 따라 달라지지 않는 일'을 말한다고 한다.
즉, 어느 방향에서 쳐다보든 상관없이 물체의 물리적 성질은 똑같이 보인단 소리다.
비등방성의 대표적으로 지폐의 표면에 붙은 홀로그램이 있다.
보는 각도에 따라 다른 성질을 보이고 있는 것이 '비등방성(anisotropy)'이라는 뜻이다.
영문위키에서도 아래와 같이 설명하고 있다.
"Anisotropy /ˌænɪˈsɒtrəpi/, /ˌænaɪˈsɒtrəpi/ is the property of being directionally dependent, which implies different properties in different directions, as opposed to isotropy. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties (absorbance, refractive index, conductivity, tensile strength, etc.)"
비등방성은 굴절률이나 conductivity등의 예도 들 수 있다는데,
알고 싶었던 부분이 바로 이 부분이었다.
Gas chromatography에서 흔히 사용됐었던 detector로
TCD (Thermal Conductivity)라는게 있었다.
TCD는 두 개의 평행한 튜브가 가스를 운반하고, 코일에 의해 가열되는 구조라고 한다.
이렇게 생겼다.
왼쪽 관으로 reference column으로부터 나온 pure carrier gas가 흘러가고
오른쪽 관으론 analytic column에서 온 sample + carrier gas가 흐른다.
그리고 두 관에서 나온 가스들을 코일로 가열시켜서 heat loss rate를 측정한다.
두 관에서 온 가스의 열전도율이 다르다는 점에서 착안,
그 미묘한 차이를 측정한다는 원리로 탄생한 detector가 바로 TCD이다.
같은 문서에서 부가 설명하길
대부분 화합물들은 일반적으로 사용되는 hydrogen이나 helium같은 carrier gas들에 비해
conductivity가 훨씬 낮다고 한다.
그러니까 시료가 들어있는 column에서 온 gas의 conductivity가 훨씬 낮을테니
그 차이를 전기적으로 측정하면 되는 것이다.
그래서 conductivity에 있어서 anisotropy라는건 무엇을 뜻하는걸까?
그래서 다시 찾아보았다. Isotropic/anisotropic thermal conductivity는 무엇이 다른걸까..
아래와 같은 답변은 찾을 수 있었다.
""Anisotropic" means the thermal conductivity of the material depends on the direction the heat flows through the material. It can also cause strange behaviour where the heat does not flow in the same direction as the temperature gradient. Most common materials are isotropic. If your material data doesn't include anisotropic thermal properties, just ignore the option."
비등방성이란건 물질의 열전도율이 열이 흐르는 방향에 의존적이게 나타난다는 뜻입니다. 열이 높은 곳에서 낮은 곳으로 이동하는 구배에 따라 흐르지 않을 때 발생할 수 있습니다. 대부분의 물질은 등방성을 띱니다. 당신의 물질 데이터가 비등방성 열전도의 속성을 보이거든, 옵션을 무시하세요
옵션(?)이 뭔진 모르겠지만, 열이 이동함에 있어서
항상 고온에서 저온으로 이동하지만은 않는단걸 얘기하는 듯하다.
열의 이동도 하나의 '방향'으로 생각할 수 있다. 그런데 그 열의 이동방향에 따라
물질의 열전도율이 다르게 측정된다는 점이 anisotropic의 개념인 듯하다.
정확하게는 뭔소린가 잘 모르겠다 솔직히는...
그래서 더 찾아보았다. 완전하게 이해가 갈 때까지 찾아보려 한다.
다른 사이트를 참조했다.
열이 고온에서 저온으로 이동하며 평형을 이루게 됨은 누구나 아는 사실이다.
한편 열전도율은 온도 경사에 따른 열의 흐름 속성을 나타내는 말이다.
J는 열 흐름, k는 열전도율, dT/dr은 온도 구배이다.
석영에서 c축과 수직인 경우엔 conductivity가 6.5 Wm^-1K^-1이다.
하지만 c축과 평행할 때에는 11.3 Wm^-1K^-1까지 상승한다.
아하! 이 화합물은 방향에 따라 열전도율이 달라졌다.
석영 크리스탈을 c 축과 수직으로 하나 자르고, 평행하게 하나 더 잘라놓는다.
두 조각을 수직으로 배치하고, 가운데에 열원을 둔다.
철을 데우면 가운데서부터 열을 받아서 전도되는 모습을 볼 수 있다.
동영상 참조
"방향에 따라 열전도율의 차이가 생긴다"라는 것이
heat conductivity에 있어서의 anisotropy의 개념이다.
이 개념으로 TCD의 사진을 다시 한 번 보면 조금 더 이해가 된다.

열 전도율이 다를테니 아래로부터(혹은 위로부터) 반대방향으로 열이 전달될 때
carrier gas보다 sampl + carrier gas의 열전도율이 낮을 것이다.
그 다른 정도를 옆의 detector가 전류의 흐름을 감지해서 구분해낸다.
이제야 이 사진이 전부 이해되었다.
2018-10-28
HTML, CSS 강좌 사이트 추천
HTML이 뭔지도 모르겠고, 처음 접해보는 사람이라면
아래의 주소를 추천합니다.
http://webberstudy.com/html-css/beginning/introduce/
구름edu (실습환경 제공)
이제 막 XML이 어떻게 생긴 것인지 알아갈 때 즈음
HTML이랑 형식이 너무나도 비슷하게 생겼다는 것을 느끼게 되었다.
비전문가가 보기엔 그냥 똑같이 보인다...
그래도 분명히 차이점은 있다고 한다.
1. HTML은 데이터의 표현에 그 목적을 두고 있고
XML은 데이터 교환을 위한 구조정의에 목적이 있다.
2. HTML이 정해진 태그를 가지고 표현하는 것이라면
XML은 사용자가 태그를 정의해서 사용할 수 있다.
3. HTML이 인터넷 웹 환경에서 작동되는 언어라고 본다면
XML은 어느 특정 환경에 구애를 받지 않는다.
4. HTML이 데이터와 그 표현을 동시에 하고 있다면
XML은 데이터만 가지고 있을 뿐, 그 표현을 하고 있지 않다.
즉, 마크업 언어(markup language)라는 점은 같다보니 형식이 비슷하게 보이긴 하지만
그 목적이 완전히 다르다는 것을 알 수 있었다.
HTML은 '미리 정해진 태그'가 있다는 점을 주목해야 한다.
그 '미리 정해진 태그'를 공부해야 하는 것이
XML과 다른 점이다.
아래의 주소를 추천합니다.
http://webberstudy.com/html-css/beginning/introduce/
구름edu (실습환경 제공)
이제 막 XML이 어떻게 생긴 것인지 알아갈 때 즈음
HTML이랑 형식이 너무나도 비슷하게 생겼다는 것을 느끼게 되었다.
비전문가가 보기엔 그냥 똑같이 보인다...
그래도 분명히 차이점은 있다고 한다.
1. HTML은 데이터의 표현에 그 목적을 두고 있고
XML은 데이터 교환을 위한 구조정의에 목적이 있다.
2. HTML이 정해진 태그를 가지고 표현하는 것이라면
XML은 사용자가 태그를 정의해서 사용할 수 있다.
3. HTML이 인터넷 웹 환경에서 작동되는 언어라고 본다면
XML은 어느 특정 환경에 구애를 받지 않는다.
4. HTML이 데이터와 그 표현을 동시에 하고 있다면
XML은 데이터만 가지고 있을 뿐, 그 표현을 하고 있지 않다.
즉, 마크업 언어(markup language)라는 점은 같다보니 형식이 비슷하게 보이긴 하지만
그 목적이 완전히 다르다는 것을 알 수 있었다.
HTML은 '미리 정해진 태그'가 있다는 점을 주목해야 한다.
그 '미리 정해진 태그'를 공부해야 하는 것이
XML과 다른 점이다.
2018-10-27
XML 공부하기
파이썬을 공부하다가
즉, XML이란건 그 자체로서 데이터들을 관리하는 언어가 아니라
다른 언어를 만드는 메타-언어라는 것이다.
XML을 기반으로 한 특수 목적용으로 제작한 언어들도 있는데
그게 DTD, XML Schema를 작성하고 표준으로 제정한 것이라고 한다.
RSS가 바로 이 XML을 기반으로 한 '데이터 기술 언어'라고 한다.
RSS는 Rich Site Summary의 약자라고 한다.
편의상 그냥 전부 XML이라고 부르는 것 같다.
그러면 XML은 어떻게 생겼을까?
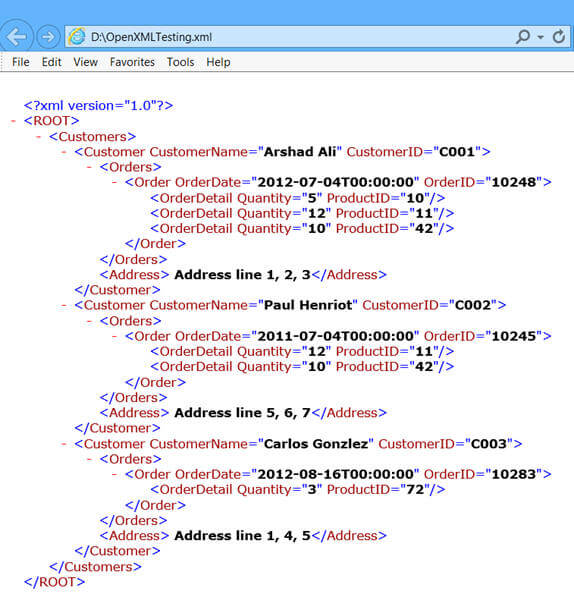
대략 이렇게 생겼다고 한다.
제일 첫줄엔 이라는 식으로 이 문서가 xml 형식이라는걸 적어주고
그 다음엔 ROOT라는 것(?) 이하로 쭉 펼쳐져있는 나뭇가지같이 생겼다.
저걸 뭐라고 부르는걸까??
을 시작 태그의 예시로 들고 있으며, 을 끝태그라고 예시하고 있다.
The Great Gatsby

- "학생증"
파이썬으로 XML을 처리하는 방법에 관한 부분이 있어서
조금 더 근본적인 호기심이 들기 시작했다.
'XML이 뭐지??'
XML이라는건 markup language로 만든 문서를 말한다.
그래서 XML은 그 자체로 '문서'로 칭해진다.
그러면 XML은 HWP, DOCS, HTML 파일처럼 작성되어있는 문서라는 뜻인걸까?
위키에서는 이렇게 얘기하고 있다.
"XML(Extensible Markup Language)은 W3C에서 개발된,
다른 특수한 목적을 갖는 마크업 언어를 만드는데 사용하도록 권장하는
다목적 마크업 언어이다."
즉, XML이란건 그 자체로서 데이터들을 관리하는 언어가 아니라
다른 언어를 만드는 메타-언어라는 것이다.
XML을 기반으로 한 특수 목적용으로 제작한 언어들도 있는데
그게 DTD, XML Schema를 작성하고 표준으로 제정한 것이라고 한다.
RSS가 바로 이 XML을 기반으로 한 '데이터 기술 언어'라고 한다.
RSS는 Rich Site Summary의 약자라고 한다.
편의상 그냥 전부 XML이라고 부르는 것 같다.
그러면 XML은 어떻게 생겼을까?

대략 이렇게 생겼다고 한다.
제일 첫줄엔 이라는 식으로 이 문서가 xml 형식이라는걸 적어주고
그 다음엔 ROOT라는 것(?) 이하로 쭉 펼쳐져있는 나뭇가지같이 생겼다.
저걸 뭐라고 부르는걸까??
라고 적어둔 부분은 'XML 선언부'라고 한다.
이 구절을 통해 "이 문서는 XML 문서입니다"라는걸 알려주는 셈이다.
Markup과 content.
XML 문서는 <와 >로 감싼 부분들이 있다. 그 부분을 '마크업'이라고 부르는 것 같다.
예를 들어서 위의 짤에
부터 사이에 들어가는 내용들이
부터 사이에 들어가는 내용들이
아마도 content라고 부르는 부분인 것 같다. 그리고 / 기호는
그 구절이 끝났음을 알려주는 표시인 것 같다.
그래서 <로 시작해 >로 끝나는 마크업 구조를 태그(tag)라고 부르고
빈 엘리먼트(empty-element)라는건 해당 마크업은 있지만 내용이 없는걸 일컫는 것 같다.
엘리먼트(Element)라는건 문서의 논리 요소로서,
시작 태그로 시작하여 짝이 되는 끝태그로 끝나거나,
빈 엘리먼트 태그만으로 이루어진 블록(?)을 말하는 것이다.
내가 보기엔 꼭 시작태그~내용~끝태그의 모양이 하나의 레고 블럭같이 보였다.
엘리먼트 내부에 또다른 엘리먼트를 넣는 것이 가능하다.
자식 엘리먼트를 포함시킬 수 있다는 것이다.
이렇게 계층구조를 만들 수 있는데,
문서 내에서 최상단 계층을 ''루트 엘리먼트(root element)"라고 부르며
루트 엘리먼트는 문서에서 단 한 개밖에 없다고 한다.
엘리먼트 내부에 다른 엘리먼트를 가질 수도 있지만, 그 안에 내용을 집어넣을 수도 있다.
책의 이름이 '위대한 개츠비'라고 표현한 것이다.
엘리먼트는 스스로의 정보를 나타내는 속성(attribute)을 가질 수 있다.
예를 들어서 이 짤에서는

루트 엘리먼트 아래에 Customers 엘리먼트가 있고
해당 엘리먼트는 Orders와 Address라는 자식 엘리먼트를 갖고 있으며
자체적으로 CustomerName과 CustomerID라는 어트리뷰트를 갖고 있다.
또한, 자식 엘리먼트였던 Orders는 그 아래로 Order라는 엘리먼트를 갖고 있으며
Order 엘리먼트는 OrderDate와 OrderID라는 어트리뷰트를 갖고 있다.
나의 감각으로는 마치 이런 것처럼 받아들였다 :
어트리뷰트는 그 엘리먼트의 이름표와 같다.
고등학생이 갖고 있는 속성으로는 '교복을 입는다', '나이가 보통은 17~19세다'
등등이 있는데, 그 속성들을 정의하고 있는 것이다.
루트 엘리먼트 아래로 수많은 학생이 들어갈 수 있겠지만
그 중에 '익명' 학생에 대해 작성해본 것이다.
그 학생의 이름은 '익명'이고, 나이는 '19'다.
그 학생이 소지하고 있는 것은 '학생증'이다.
그리고 손으로 타자를 쳐보면서 알게 된 점인데...(이래서 눈코딩보다 손코딩이 좋다)
어트리뷰트는 스페이스바(whitespace) 공간으로 구분하고 있다.
저 짧은 문서만 손으로 작성해보아도 감이 올거라 생각한다.
그래서 어느정도 용어에 관한 감이 생겼으니
다른 문서도 보기로 했다.
문법에 맞는 XML 문서란건...
XML 문서로서 가져야 하는 필수 요건을 갖춘 문서를 지칭한다.
그 필수 요건은 다음과 같았다.
1. 루트(Root) 요소를 하나만 가져야 합니다.
2. 모든 XML 요소는 종료 태그('끝태그'인듯)를 가져야 합니다.
3. 시작 태그와 종료 태그에 사용된 태그 이름이 대소문자까지 완벽하게 일치해야 합니다.
4. 모든 XML 요소의 여닫는 순서가 반드시 정확하게 지켜져야 합니다.
5. 모든 속성의 속성값이 따옴표로 둘러싸여 있어야 합니다.
위의 예시로 작성한건 이 중에 하나라도 어긋나는게 없는
'매우 잘 만든 문서'였다.
일단 기본적인 개념은 이렇게 알아들으면 되겠다.
엘리먼트? 어트리뷰트? 서브 엘리먼트?
그게 뭔가 했는데 이제 좀 감이 잡힌다.
..여담으로 XML에 관련된 그 RSS를 알아보다가
RSS의 개발 초기단계에 관여했던 애런 스워츠(Aaron Swartz)에 관한 글을 읽게 됐다.
2018-10-19
Pycharm에서 자주 쓰는 단축키들
Tab : 문장을 지정해둔 상태로 tab 키를 누르면 해당 문장을 들여쓰기함.
Shift + Tab : tab으로 들여쓰기한 문단을 다시 한 수준 아래로 내릴 때 사용.
Shift + Enter : Jupyter notebook에서 해당 라인을 실행한 후 다음 라인을 생성
Ctrl + Enter : 해당 라인만 실행시킴. 다음 라인을 생성하지 않음.
2019.1 버전부터 파이참 내의 주피터 노트북 사용이 유료로 전환됨.
Esc : 해당 라인을 수정하다가 esc 키를 누르면 수정 상태를 빠져나와 라인별 이동 가능
방향키 위, 아래 : 라인별로 이동 가능.
Enter : 라인별로 이동하다가 Enter를 누르면 해당 라인을 수정하러 들어갈 수 있음.
Shift + F6 : 해당 변수의 이름을 모든 위치에서 한 번에 변경할 수 있다.
Ctrl + Q : 해당 함수의 quick documentation을 볼 수 있다.
(커서가 메서드를 가리킬 때)
Ctrl + Q : Quick Documentation
Ctrl + Shift + Space : 매개 변수 정보
Ctrl + P : 현재 함수(혹은 메서드)의 파라미터 목록
F12 : 메서드 정의로 이동
Ctrl + w : 구역 설정
(Regular Expression 사용시)
Alt + Enter : Match되는 문자열을 테스트해볼 수 있다.
Alt + 7 : 변수의 사용처를 추적할 수 있다.
Ctrl + B : 해당 문서로 빠르게 이동.
Shift + Tab : tab으로 들여쓰기한 문단을 다시 한 수준 아래로 내릴 때 사용.
2019.1 버전부터 파이참 내의 주피터 노트북 사용이 유료로 전환됨.
Esc : 해당 라인을 수정하다가 esc 키를 누르면 수정 상태를 빠져나와 라인별 이동 가능
방향키 위, 아래 : 라인별로 이동 가능.
Enter : 라인별로 이동하다가 Enter를 누르면 해당 라인을 수정하러 들어갈 수 있음.
Shift + F6 : 해당 변수의 이름을 모든 위치에서 한 번에 변경할 수 있다.
Ctrl + Q : 해당 함수의 quick documentation을 볼 수 있다.
(커서가 메서드를 가리킬 때)
Ctrl + Q : Quick Documentation
Ctrl + Shift + Space : 매개 변수 정보
Ctrl + P : 현재 함수(혹은 메서드)의 파라미터 목록
F12 : 메서드 정의로 이동
Ctrl + w : 구역 설정
(Regular Expression 사용시)
Alt + Enter : Match되는 문자열을 테스트해볼 수 있다.
Alt + 7 : 변수의 사용처를 추적할 수 있다.
Ctrl + B : 해당 문서로 빠르게 이동.
2018-09-12
구글 문서도구(Google Docs)에서 이미지 추출하는 방법
구글 드라이브에서 함께 서비스되고 있는 구글 문서도구(Google Docs).
이미지를 삽입하기는 참 쉽다.
윈도우 폴더에서 사진 파일을 드래그&드랍해서 문서 안에 '던져넣'으면 된다.
근데 문제는, 그 삽입된 이미지를 다시 윈도우 폴더로 가져올 수가 없다는 점이다.
그래서 검색해보았다. How to extract the image from Google Docs?
아래의 내용은 5 Quick Ways to Extract and Save Images from Google Docs
에서 알려준 방법을 토대로 작성되었다.
1. 웹에 게시하기
이 방식은 '추출하고자 하는 이미지가 적을 때'에 사용하기 좋다.
파일 - 웹에 게시
게시 클릭
링크를 복사해서 새 창으로 들어가보면
이미지를 우클릭해서 다운받을 수 있다.
다 뽑았으면 게시 중지를 눌러서 마무리
적은 이미지를 선택적으로 다운받고 싶을 때 쓰기 좋은 방식.
2. 웹 페이지로 다운받기
문서에 사진이 많을 때 일괄적으로 모든 사진을 다운받을 수 있는 방법.
파일 - 다른 이름으로 다운로드 - 웹페이지(압축됨) 클릭
다운받아진 압축파일을 열면
'image' 폴더에 모든 사진이 담겨있는걸 확인할 수 있음.
3. 이미지 추출 부가기능 사용하기
많은 이미지를 다운받아야 하지만 전부 다운받을 필요는 없을 때.
부가기능 - 부가기능 열기 클릭
검색창에 'image extractor'라고 검색
그리고 해당 부가기능을 잘 사용하면 된다.
4. 해당 사진을 스샷으로 찍어버리기
적은 개수의 이미지를 고해상도로 추출하고 싶을 때 사용함.
윈도우 사용자의 경우엔 키보드의 'Print Screen Sys Rq' 혹은 'PrtScr'같은 키를 누르면
해당 화면을 클립보드에 복사해서 그림판 등에서 사용할 수 있다.
Mac 사용자는 Shift + Command + 4 라고 한다.
5. 마이크로소프트 워드 파일로 다운받아서 이미지를 추출하기
이 방법은 Google Doc에서 마이크로소프트 워드로 옮겨가서 작업하고 싶을 때 사용함.
파일 - 다른 이름으로 다운로드 - 마이크로소프트 워드 클릭
다운 받아진 파일을 열어서 작업
이렇게 다운받아서 사용할 수 있다.
가장 기호에 맞는 방식을 골라 사용하면 될 듯 하다.
피드 구독하기:
덧글 (Atom)